期权定价中的希腊值有什么用？-期货学堂-18期货网

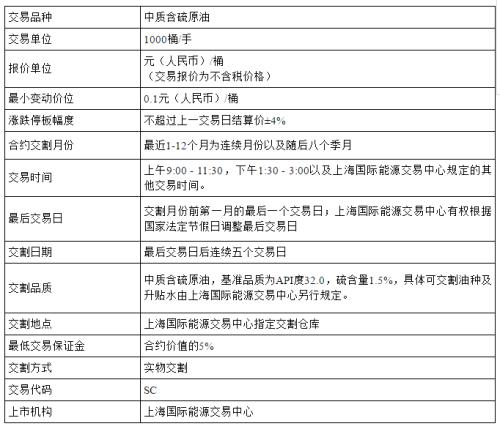
期权价格由标的价格、到期时间、波动率三个因素决定，这已是老生常谈。理论上来讲，期权定价公式可以表示为，以标的价格(f)、到期时间(t)、波动率(σ)三个因素为自变量，期权价格为因变量的多项式。

何为希腊值

P=Ax+By+Cz (1)

而这个公式我们就熟悉多了，只要知道了A、B、C三个系数，无论x、y、z怎样变化我们都可以求得对应的P值。这里x、y、z三个自变量就是f、t、σ三个因素，P就是对应的期权价格。当然，在实际当中P与 f、t、σ三个因素间是更为复杂的非线性关系。

P=Af+Bt+Cf2+Dσ+…… (2)

公式后面省略了很多f、t、σ的高阶项，因为阶数的增加对P的影响会越来越小。随着标的价格变化、到期时间衰减、波动率涨跌，我们就可以通过公式(2)简单估算出期权价格的变化。

△P=A△f+B△t+C(△f)2+DAσ (3)

读到这里，你会发现期权定价好像并没有想象中的复杂。如果精度要求不高，可以通过公式(3)简单进行估算，从而预估在不同情形下头寸的损益。

这种情景分析正是风险控制的重要一环，只要将预想中最有利的情况与最不利的情况都代入公式(3)就可以得到头寸最大盈利与最大亏损的预估值。接着通过调整头寸，就可以得到理想的盈亏比，同时将最大亏损控制在可承受范围。

另外，我们可以单独分析暴露在f、t、σ上的风险。这个过程更为简单，从公式(3)中可以看出，f变动对于P的影响程度完全取决于A的大小，因此A就是期权头寸在标的涨跌方面暴露的风险。以此类推，B就是头寸在时间流逝方面暴露的风险，D就是头寸在波动率涨跌方面暴露的风险。

那么现在的关键就是A、B、C、D分别都是什么呢？又怎么计算呢？

其实，它们都属于本文的主角，也就是“希腊值”。公式(2)中省略了很多f、t、σ的高阶项，这些高阶项前面也都有各自的“希腊值”。为了区分这些“希腊值”我们给它们起了不同的名字，我们通常用到的A、B、C、D分别叫做 Delta、Theta、Gamma、Vega，其中只有Gamma是二阶的希腊值，对于入门投资者来说可以放在最后学习。它们的计算在基础的期权定价课本中都有涉及，我们这里不做赘述。在实际交易当中，专业的期权交易软件也都会提供计算好的“希腊值”，因此大家也不必担心，只需要会用即可。

希腊值的两个要素

每个希腊值都有两个要素：一是符号(+/-)，二是数值。

1.Delta

(1)符号

“+”代表做多标的物，例如：买入Call、卖出Put 做多标的物，Delta为正值；

“-”代表做空标的物，例如：卖出Call、买入Put 做空标的物，Delta为负值。

(2)数值

Delta数值的理解有两种角度。

期权的Delta值代表其在方向交易上等于多少份等合约价值的期货。举例：

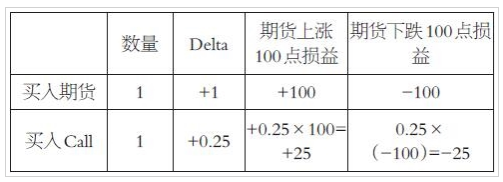
期权定价中的希腊值有什么用？

同时，期权的Delta值代表到期日它进入实值的概率。

任何时期，买入平值Call，Delta = +0.5 ；买入平值Put，Delta = -0.5；

临近到期，实值+Call Delta = +1 ；实值+Put Delta = -1.

2.Vega

(1)符号

“+”标的超预期波动，隐含波动率上涨时赚钱，例如：买入Call、买入Put时Vega为正值；

“-” 标的预期内振荡，隐含波动率下跌时赚钱，例如：卖出Call、卖出Put时Vega为负值。

(2)数值

隐含波动率增加时期权价格上涨的数值。举例：

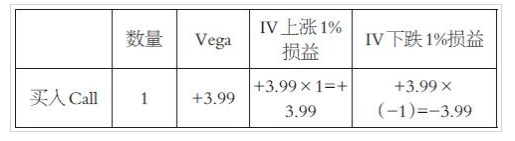
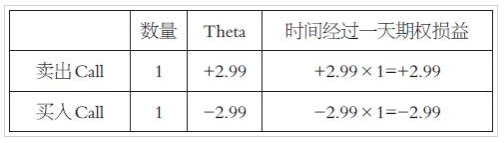
期权定价中的希腊值有什么用？

3.Theta

(1)符号

“+” 卖期权收取的权利金逐日转为已实现收益，例如：卖出Call、卖出Put时Theta为正值；

“-” 买期权付出的权利金逐日转为已实现亏损，例如：买入Call、买入Put时Theta为负值。

(2)数值

随时间流逝，期权权利金衰减的数值。举例：

期权定价中的希腊值有什么用？

希腊值的理解与应用

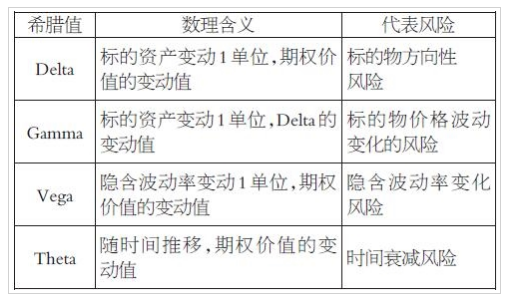
期权定价中的希腊值有什么用？

希腊值都有一个非常棒的共性，就是标准化可以加减。无论是不同行权价，还是不同到期日，任何期权合约的希腊值都可以加总起来，从而得到总持仓的汇总希腊值，也就是得到了整体头寸的风险暴露情况。

当然，不同的希腊值所代表的风险暴露情况也不同。

通常我们会使用专业期权软件自带的希腊值汇总功能来分析头寸的风险暴露情况。

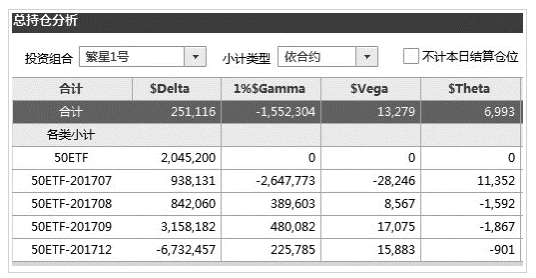
下图是某一交易日实际持仓的希腊值情况。从“合计”一行的汇总希腊值可以看出，(1)Delta值为正，即标的物上涨获利，下跌亏损；(2)Vega值为正，即期权IV整体上涨获利，下跌亏损；(3)Theta值为正，即随着时间流逝，会有额外的时间价值转为收益。

另外，我们也会关注不同月份的风险状况。以1707合约为例：(1)Delta值为正，标的物上涨对1707合约持仓有利，标的下跌则亏损；(2)Vega为负与总体持仓不同，即1707合约IV整体上涨1707合约持仓亏损，IV下跌则获利；(3)Theta为正，即随着时间流逝，1707合约持仓会有额外的时间价值转为收益。

期权定价中的希腊值有什么用？